人工知能(AI)は今日、至るところに存在しています。
AIは、これまでにない方法でトレンドを発見し、パターンを見つけ、問題解決に貢献しています。
医療から小売、研究まで、AIは新たな可能性を切り開いています。
しかし、重要なのはAIはデータの質に依存するということです。
モデルのトレーニング、類似性検索の実行、あるいは人間が理解できる応答を生成するための生成AIの使用など、一般的により多くのデータがあれば、より良い結果が得られます。
大規模言語モデル(LLM)のようなツールが重要になってくるのはこのためです。
これらは巨大なデータセットで訓練され、ほぼ人間のような回答を生成することができます。
素晴らしいと思いませんか?
ただし注意点があります。
LLMは必ずしも正確な答えを出すとは限りません。
追加のコンテキストによる指針がない場合、不完全な回答や、「ハルシネーション」と呼ばれる完全な作り話を返すことがあります。
ここで、関連するコンテキストを提供することが大きな違いを生みます。
では、これらのモデルにどのようなコンテキストを与えるべきかをどのように判断すればよいでしょうか。
ここでベクトル、ベクトル検索、ベクトルデータベースが重要になってきます。
従来のキーワード検索とは異なり、ベクトル検索は単なる単語の一致ではなく、意味に焦点を当てることができます。
ベクトルデータベースは、コンテキストを重視した方法でデータを保存・検索します。
本記事では、ベクトルとは実際に何か、それがどのように機能するのか、そしてなぜ開発者がよりスマートで信頼性の高い生成AIシステムを構築する上で重要になっているのかを詳しく説明します。
ベクトルとは何か?
ベクトルデータベースと生成AIにおけるその役割について詳しく説明する前に、まず基本的なところから始めましょう。
ベクトルとは一体何を指すのでしょうか?
オンラインで検索すると、以下のような定義が見つかります。
ベクトルは、データを表現し整理するための数学的アプローチです。単語のベクトル化などのデータのベクトル化は、MLモデル作成の初期段階の一つです。 – H20.ai
人工知能において、ベクトルはAIアルゴリズムが理解できる形式でデータを表現する数学的な点です。ベクトルは数値の配列(またはリスト)で、各数値がデータの特定の特徴や属性を表します。 – MongoDB
これらの定義は正確ですが、正直なところ、初心者にとって分かりやすいものではありません。
もっと簡単に説明しましょう。
ベクトルは単に順序付けられた一連の数値です。
したがって[1.5, 2.5, 3.0]はベクトルの例であり、[3.0, 1.5, 2.5]も同様です。
ベクトル内の数値の順序が重要なため、これら2つのベクトルは同じ数値を含んでいても異なるものとみなされます。
重要な用語として、ベクトルの次元性があります。これは単にベクトル内の数値の数を指します。
これらのサンプルベクトルはどちらも3次元です。
かなり簡単ですよね!
しかし、これだけではなぜベクトルが有用なのか、どのように形成されるのかについては説明できていません。
説明のために、簡単な例を見てみましょう。
ベクトルの例を家探しに例える
あなたは今、家を探しているとしましょう。
特定の郊外に絞り込み、床面積約2,500平方フィート(ft2)、敷地面積6,500ft2の家を探しているとします。
現実には、価格、寝室と浴室の数、築年数、キッチンと浴室が更新されているかなど、多くの要因を考慮する必要がありますが、この例では単純に床面積と敷地面積に焦点を当てましょう。
さらにベクトルの概念を説明するために、床面積が敷地面積の2倍重要だと仮定します。
これは、ある要素を他の要素よりも重視する重み付けを導入することを意味します。
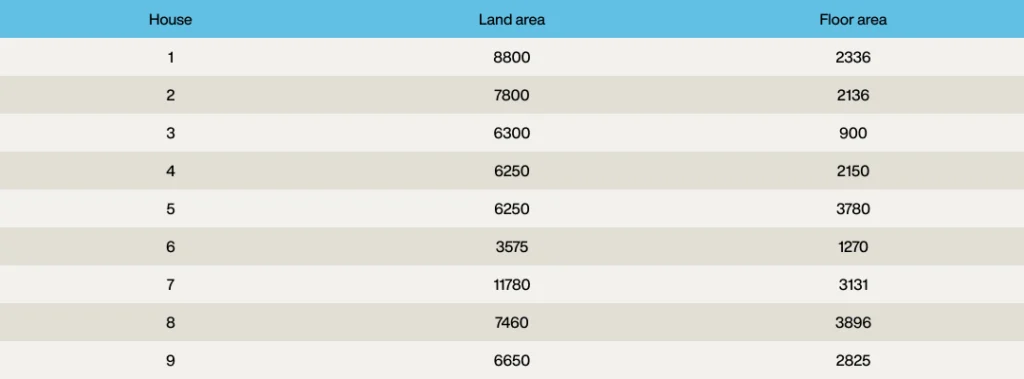
地域を絞り込んだところ、その地域には9つの物件があることがわかりました。
これらを希望する物件を赤い「x」で示したグラフにプロットするとこのようになります。
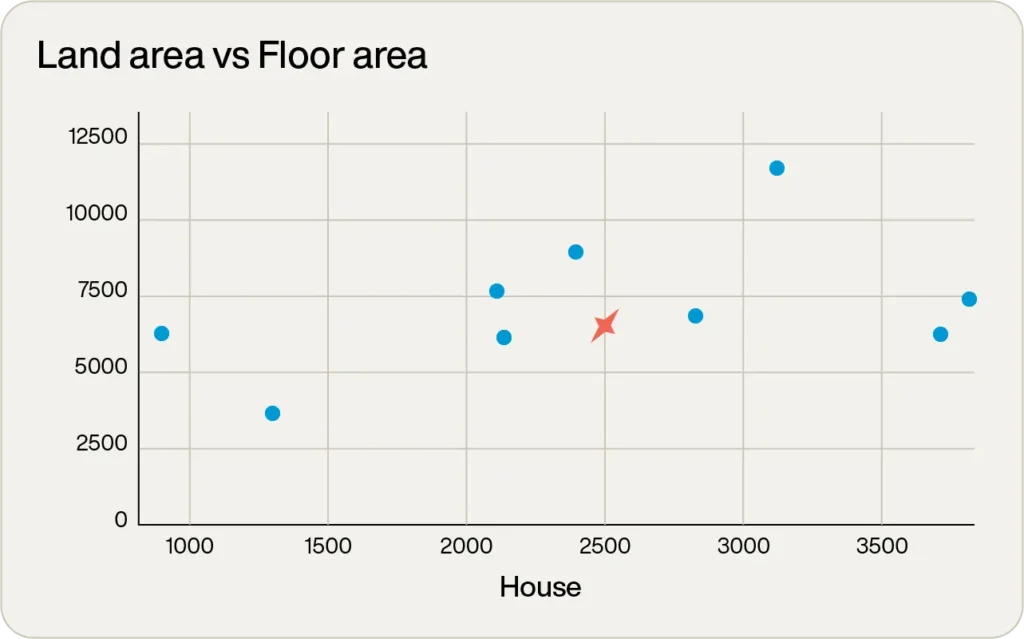
これを見ると、9つの物件のうち4つがかなり良い候補であることがわかります。
しかし、どれが「最適」でしょうか?
敷地面積と床面積という2つの属性は、実質的に2次元のベクトルを形成します。
したがって、敷地面積8,800ft2、床面積2,336ft2の最初の家は、ベクトル[8,800, 2,336]を持つことになります。
ベクトルの最初の要素が敷地面積で、2番目の要素が床面積です。
最初のステップは、各値が0から1の範囲になるようにベクトルを正規化することです。
これは厳密には必要ありませんが、ベクトルの2つの次元を簡単に比較できるようになります。
したがって、最大の敷地面積(物件7、11,780ft2)を見つけて各敷地面積をこれで割り、最大の床面積(3,896ft2)についても同様に行います。
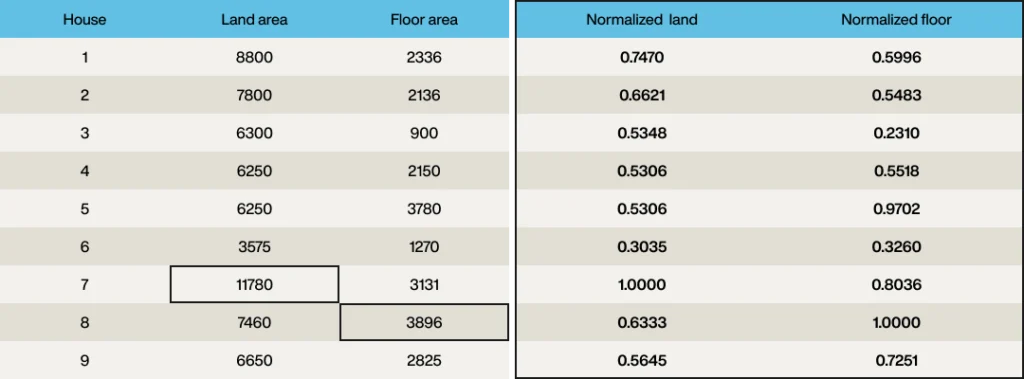
ベクトル要素は、各列が同じ範囲(0から1)を持つように正規化されました。
しかし、要件では敷地面積を床面積の半分の重要度とすることでしたので、重み付けを適用するために、ベクトルの「敷地」要素の各要素を2で割ります。
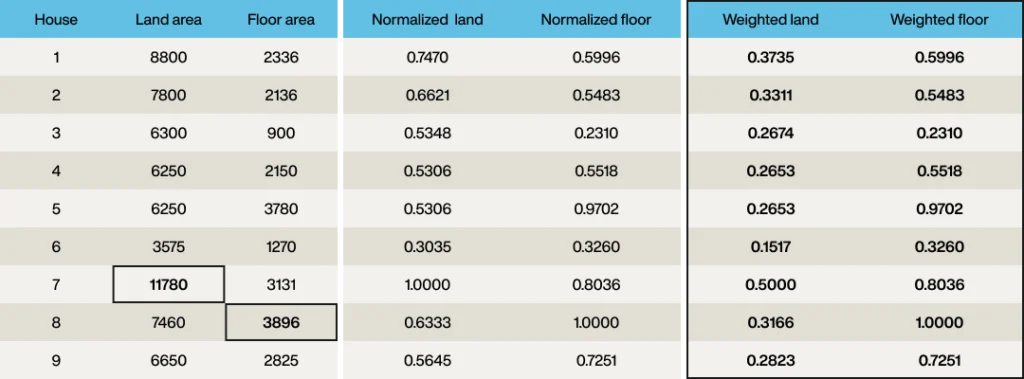
各物件は正規化されたベクトルを持つようになりました。
さて、同じプロセスを希望する要件にも適用する必要があります。
希望する床面積は2,500ft2なのでこれを3,896で割って0.6417を導き出し、希望する敷地面積は6,500ft2なのでこれを11,780で割ります。その後1/2の重み付けを適用して0.2759を得ます。
したがって、クエリベクトルは[0.2759, 0.6417]となります。
意味のある情報をベクトルに変換するプロセスは埋め込み(エンベディング)と呼ばれます。
この例では単純な埋め込みモデルを使用していますが、実際のシナリオでは通常、畳み込みニューラルネットワーク(CNN)のようなより複雑なシステムに依存します。
これらについてはこの記事の範囲を超えていますが、覚えておくべき重要なポイントがいくつかあります。
1.ベクトルはそれ自体に本質的な意味を持ちません。
[0.3735, 0.5996]というベクトルは何を意味するのでしょうか?
この例は非常に単純なので、元の床面積と敷地面積を逆算することができますが、通常はそうではありません。
ベクトルは、ドメインオブジェクトに関連付けられているからこそ有用なのです。
したがって、この場合、その特定のベクトルが物件1に関連付けられていることを知っている必要があります。
ドメインオブジェクトという用語は、ベクトルを形成するために埋め込まれたソースオブジェクトを指すために使用します。
これは、人、アカウントなどの一般的なビジネスオブジェクトのような構造化データである場合もあれば、テキスト、画像、動画などの非構造化データである場合もあります。
2.この例でのベクトル空間の次元は2つだけです。
これは通常のLLMシナリオで使用される数百から数千(またはそれ以上)の次元よりもはるかに小さいものです。
9つのベクトルを埋め込むために使用された埋め込みモデルは、ターゲットデータポイントを埋め込むために使用された埋め込みモデルとまったく同じです。
これは重要なポイントです。
ターゲット検索空間のベクトルを埋め込むために使用される埋め込みモデルがターゲットポイントを埋め込むために使用されるモデルと異なる場合、結果は無意味になります。
この結果として、埋め込みモデルから生成されるすべてのベクトルは同じ次元数を持つことになります。
ベクトル埋め込みvsベクトル表現
生成AI分野でベクトル用語を議論する際、「ベクトル埋め込み」または単に「埋め込み」という用語をよく耳にします。
しかし、時には「ベクトル表現」という用語を耳にすることもあり、これはベクトル埋め込みと同義的に使用されることがあります。
しかし、この2つの用語は同じなのでしょうか?
ベクトル表現は、モデルに関連するドメインオブジェクトのすべての「特徴」の数値表現です。
特徴という用語は単一のデータポイントを表すので、この場合、敷地面積は1つの特徴であり、床面積は別の特徴です。
ベクトル埋め込みは、類似性検索で比較できるベクトルを形成するために、ベクトル表現に行列分解技術やディープラーニングモデルを適用した結果です。
したがって、最初の物件を考えると、

[8800, 2336]がベクトル表現と考えられ、[0.3735, 0.5996]がベクトル埋め込みと考えられます(ただし、信じられないほど単純な埋め込みモデルを使用しています)。
最も近いベクトルを見つける
すべての物件(目標の物件を含む)がベクトルとしてエンコードされたので、あとはクエリベクトルに最も近いベクトルを見つけるだけです。
そうすれば、要件に最適な物件が得られるはずです。
これは「ベクトル検索」または「類似性検索」と呼ばれます。
従来のデータベースでの検索とは異なり、正確な一致ではなく、おおよその一致を探します。
検索セットから参照ベクトルに最も近いベクトルを見つけることが目的です。
しかし、「最も近い」とは何を意味するのでしょうか?
ユークリッド距離
距離の最も直感的な定義は、いわゆるユークリッド距離で、これは定規で距離を測った場合に得られる値です。
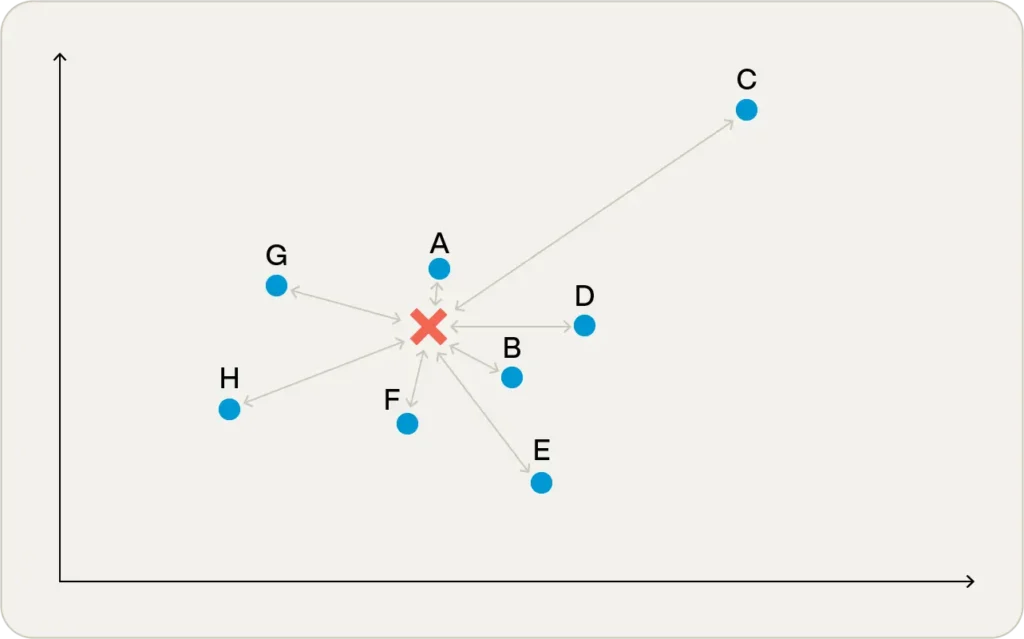
図1では、ポイントAがターゲットポイントに最も近く、ポイントCが最も遠いことがわかります。
人々は2次元グラフで見慣れているため、これを比較の明白な手段と考える傾向があります。
実際、低次元のベクトル空間では、ユークリッド距離が通常最良の結果をもたらします。
また、計算式も迅速で単純です。

これは数行のコードで実装でき、平方根の演算が最も計算コストがかかります。
しかし、必要なのはベクトル空間で最小の距離だけです。
実際の値はほとんど無関係です。
そのため、人々はしばしば計算コストの高い平方根の演算を除いた「二乗ユークリッド」距離を使用します。
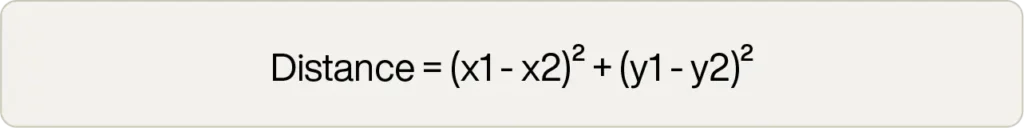
コサイン類似度
「近さ」の異なる尺度として、コサイン類似度があります。
これは説明が少し難しいです。
原点に立って異なるベクトルを見ていると想像してください。
点がどれだけ近くても遠くても、すべての点が同じ大きさだと仮定します。
つまり、あなたが気にするのはベクトル間の角度だけです。
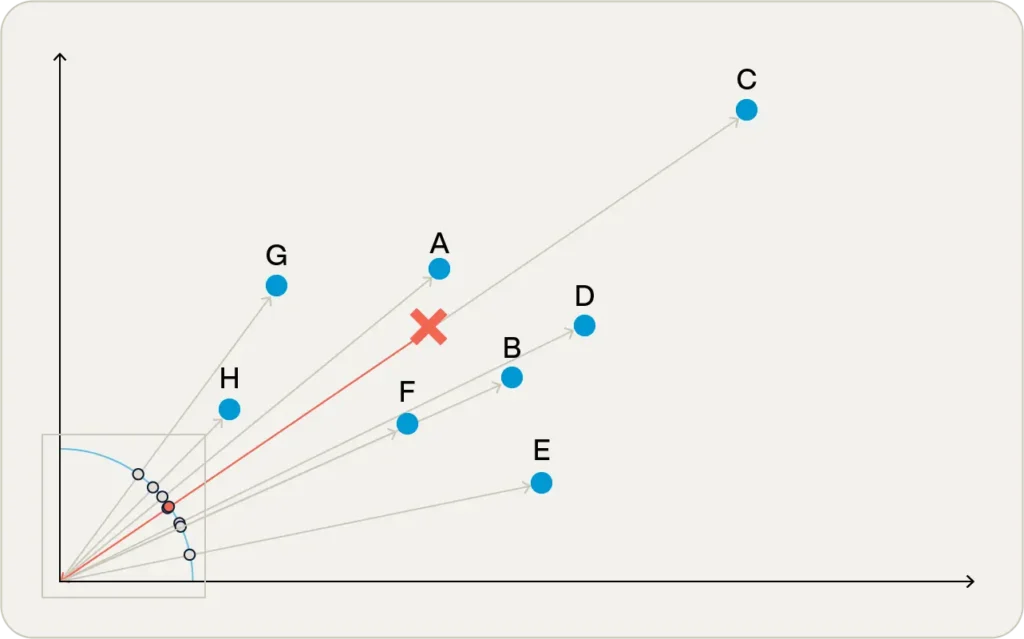
図2の原点付近の四角形を拡大すると、角度がより明確に見えます。

赤い円はターゲットベクトルへの角度を示しており、拡大図(図3)では、ターゲットベクトルとほぼ同じ角度にある点があることがわかります。
その点は実はポイントCで、奇妙なことに、ユークリッド距離法では最も遠い点でした!
このように、ベクトルの類似性を比較するために使用されるアルゴリズムの選択によって、結果は大きく異なる可能性があります。
埋め込みモデルは、しばしば最も良く機能する類似性アルゴリズムを推奨し、それらを選択するためのいくつかの経験則があります。
例えば、上で見たように、ユークリッド距離は低次元のベクトル空間でよく機能します。
コサイン類似度は高次元のベクトル空間でよく機能するため、LLMで使用される埋め込みモデルでよく使用されます。
コサイン類似度のアルゴリズムは、ユークリッド距離よりも少し複雑ですが、大きな違いはありません。数学的な定義は以下の通りです。
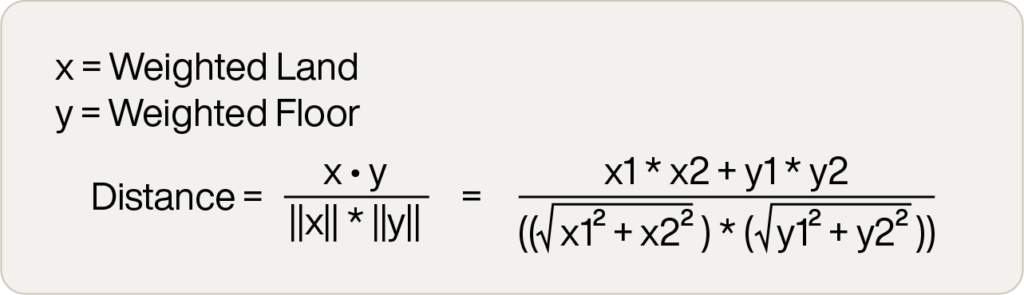
::::::::::::::::::
x ᐧ y = xとyの内積
||x|| = xの大きさ
このアルゴリズムは-1から1の範囲の数値を与え、数値が大きいほど類似度が高くなることに注意してください。
::::::::::::::::::
結果
ご存知の通り、選択された類似性アルゴリズムは結果に違いをもたらします。
ユークリッド距離は低次元のベクトル空間で最も良く機能し、この例のベクトルは2次元しかないことから、これがより良い結果をもたらすことが期待されます。
上記の公式をすべてのベクトルに適用し、目標のポイントと比較すると:
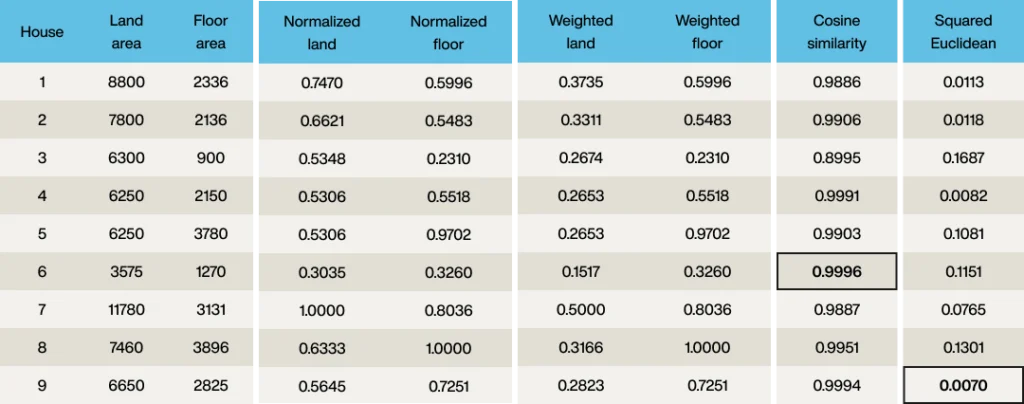
見て分かる通り、コサイン類似度では物件6がクエリベクトルに最も近い一致となり、二乗ユークリッドでは物件9が最適な一致となります。
どちらが正解なのでしょうか?そうですね、最適な物件は床面積2,500ft2、敷地面積6,500ft2を希望していました。これら2つの物件を比較すると
- 物件6は床面積1,270ft2、敷地面積3,575ft2
- 物件9は床面積2,825ft2、敷地面積6,650ft2
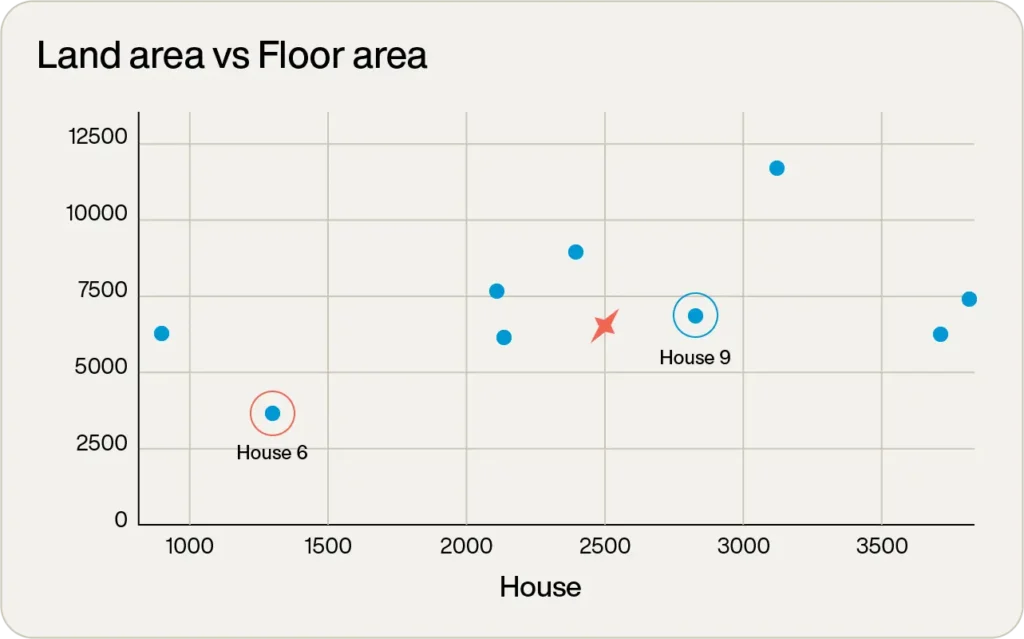
明らかに、物件9が目標の物件により良く一致しており、これは二乗ユークリッドアルゴリズムの結果から予想された通りです。
ベクトルデータベース
これまでにベクトルと類似性検索について理解を深めてきました。
これにより、ベクトルデータベースの使用について理解するための基礎が得られました。
非常に単純な見方をすれば、データベースには3つの主要な機能があります。
- ベクトルとドメインオブジェクトの両方を含む情報の保存
- 情報の取得
- 選択されたアルゴリズム(二乗ユークリッド、コサイン類似度など)を使用してデータベースに対してベクトル検索を実行し、渡されたベクトルに最も近いベクトルに関連付けられたドメインオブジェクトを取得します。返されるドメインオブジェクトの数は通常、検索のパラメータとして渡されます。
実際のベクトルデータベースにはデータセキュリティ、データガバナンス、監査制御、およびフィルタリングなどのより高度なベクトル機能など、もちろんこれ以上の複雑さがあります。
しかし、これは単純なベクトルデータベースの有用な近似となります。
素朴な実装
基本的なベクトルデータベースのこれらの要件は非常に単純なため、ほとんど自明な実装が考えられます。
情報の保存(要件1)と取得(要件2)は、ビジネスオブジェクトの一意の識別子が辞書エントリのキーとなり、ベクトルを含むその他のデータが辞書エントリの値となるような辞書のような構造で実現できます。
ベクトル検索(要件3)を実行するには、各ドメインオブジェクトと関連するベクトルを反復処理し、クエリベクトルとの類似性を計算するだけです。
アルゴリズムに渡された希望するドメインオブジェクトの数Kに応じて、最も近いK個のドメインオブジェクトを保持します。
すべてのオブジェクトが考慮された後、最も近いオブジェクトのセットを返します。
この実装は、上記のベクトル例で示したプロセスとかなり似ています。非常に単純で、うまく機能します。
しかし、規模が大きくなると効率的ではありません。
数百または数千のドメインオブジェクトがある場合、それらすべてを反復処理して類似性スコアを計算することはCPU集約的ですが、すぐに完了するはずです。
しかし、10億のベクトルがある場合はどうでしょうか?または1兆個の場合は?
このような規模では、ベクトル検索に対するこの総当たりアプローチは、完了までに法外な時間がかかるでしょう。
インデックスベースのアプローチ
ほとんどの従来のデータベースと同様に、ベクトルデータベースはベクトルとそれに関連するドメインオブジェクトの取得を高速化するためにインデックスを使用します。
ただし、インデックスは通常、NoSQLまたはリレーショナルNoSQLデータベースで使用される構造とは大きく異なります。
数学の専門家の方々に向けて言えば、ベクトルデータベースのインデックスは、ベクトルの次元であるNのN次元空間上の幾何学的インデックスです。
ベクトルデータベースのインデックス作成で最も一般的なアプローチの1つは、階層的ナビゲーション可能スモールワールド(HNSW)インデックスです。
このグラフベースのアルゴリズムは、大規模なベクトル空間でも非常に高速な取得時間と高い精度を持っています。
このインデックスがどのように機能するかを高レベルで理解するために、先ほどの例を考えてみましょう。
しかし今度は、9つの物件ではなく、数百の物件から選択するとします。
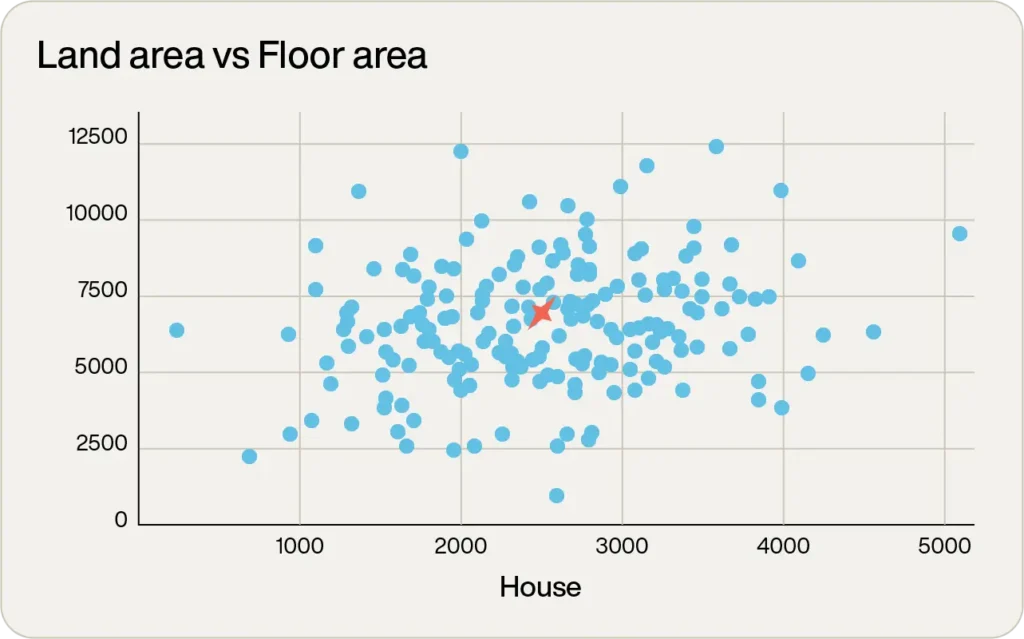
グラフを単に見るだけでも、明らかに候補にならないものがいくつかあります。
右端にある床面積5,000tf2以上の1つは大きすぎます。左端にある床面積がほとんどないものは小さすぎるでしょう。
実際、見ただけで、視覚的に領域を分類することができます。
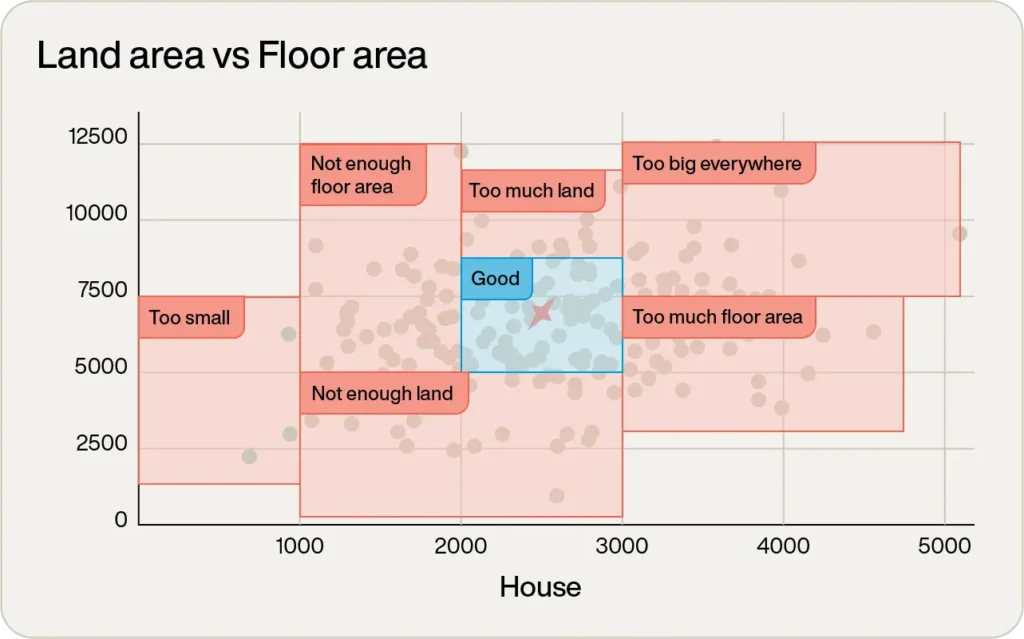
::::::::::::::::::
中央の青い四角の中にないものは安全に無視できます。
素晴らしい!単純な検査で、データポイントの大部分が除外されました。次の論理的なステップは、その領域のポイントにズームインすることです(次の図の軸のスケールに注目してください)。
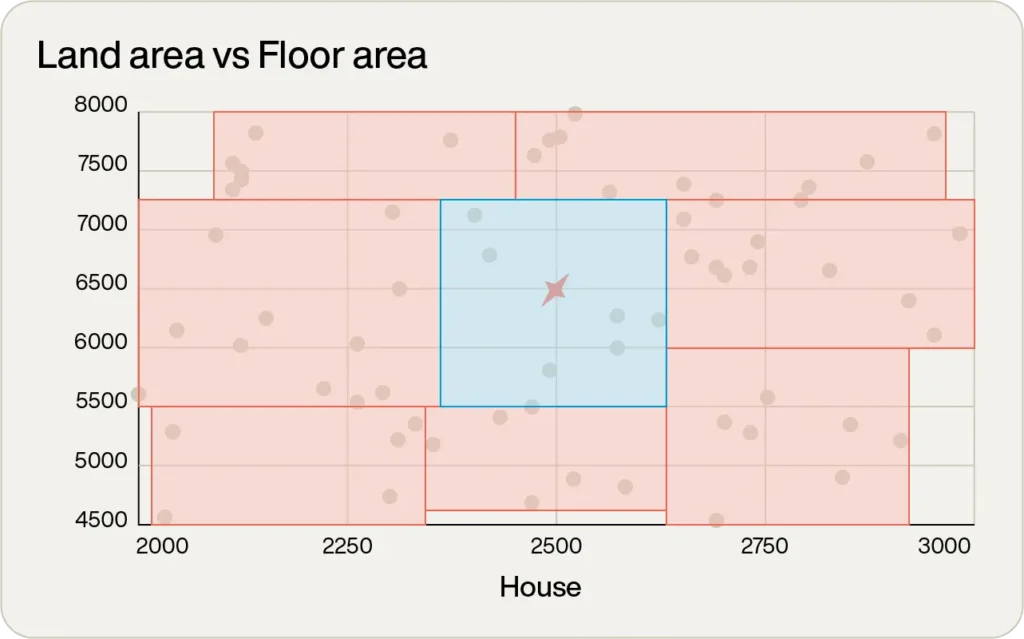
さらに拡大されたこのビューで、プロセスを繰り返します。
目標に最も近いポイントを保持し、残りを破棄します。この時点で、総当たり分析を実行するのに十分小さい8つのデータポイントまで絞り込まれました。
このプロセスは直感的に見えますが、あなたが行ったことはHNSWインデックスの動作とほぼ完全に一致します。
高レベルから始め、いくつかの非常に大きな領域を持ち、どの領域に焦点を当てるかを決定し、その領域を掘り下げ、データポイントの数が少なくなるまでアルゴリズムを再適用します。
この階層的な性質により、HNSWを以下のように描写した画像をよく目にします。
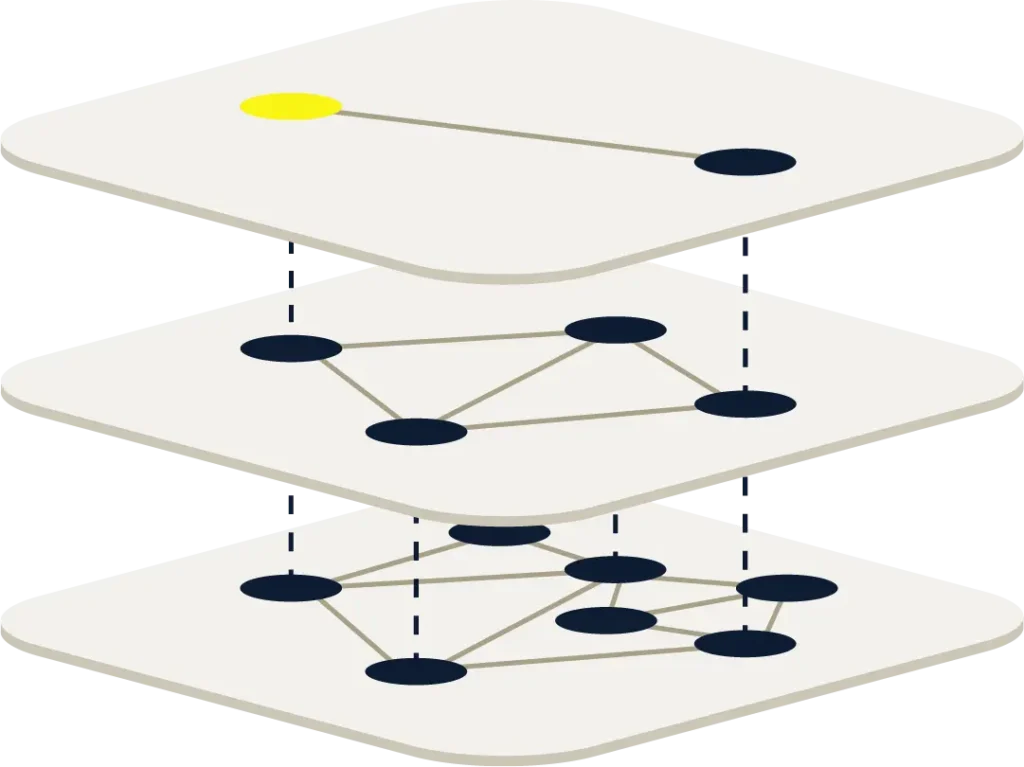
ただし、HNSWインデックスの実装は、説明は比較的簡単ですが、N次元空間での実装はより複雑です。
AIにおけるベクトルデータベースの重要性
ベクトル検索アルゴリズムはそれ自体で非常に有用です。
例えば、正確な検索語句ではなく、概念に基づいて文書のセットを検索しようとする場合を考えてみましょう。
各文書はベクトルとして埋め込まれるか、より可能性が高いのは、文書がチャンクに分割され、各チャンクがベクトルとして埋め込まれます。
これらのベクトルはベクトルデータベースに保存されます。
検索概念もクエリベクトルに埋め込まれ、類似性検索が実行されます。
これにより、クエリベクトルに最も関連する文書のチャンクに関連する類似ベクトルが得られ、結果がユーザーに表示されます。
このような「あいまい一致」は、文書と検索項目の書き記された言語をベクトル埋め込みに変換する高度なCNNを通常必要とする自然言語処理(NLP)として知られる概念であり、依然としてAIの一部です。
AIのもう一つの部分は、自然言語の書き記されたテキスト、話し言葉、生成された画像、その他の形式で、人間が理解できる応答を生成することです。
これらの応答は通常、この文書の前半で説明したLLMから生成され、生成AIとして知られるプロセスで生成されます。
LLMは非常に複雑なソフトウェアで、単純な応答を形成するだけでも数十億の計算が必要です。
これらは非常に大量のデータ(AI コミュニティではコーパスと呼ばれる)に対してディープラーニング技術を使用して作成されます。
これにより、LLMは物事を「知り」、適切な入力に対して教育的な応答を提供することができます。
しかし、これらのLLMがどんなに賢くても、いくつかの制限があります。
- 古いトレーニング:LLMは元々トレーニングされた情報のみを知っているため、その時点以降に起こったことや変更されたことについては照会できません。
- ドメイン固有の情報なし:OpenAIのChatGPTやGoogleのGemini(ほんの一例)などの公開されているLLMは、公開されているデータでトレーニングされています。これにより、トレーニング時に公開されていなかった内部メール、機密文書などのドメイン固有の情報を照会するには適していません。
- ハルシネーション:LLMがクエリに回答するための情報を持っていない状況では、もっともらしく聞こえるが完全に架空の応答を作成することがあります。これらはハルシネーションと呼ばれます。
これらの問題はすべて、質問に加えてLLMにコンテキスト情報を提供することで解決できます。
このコンテキスト情報は通常、意味検索で照会されたベクトルデータベースから得られます。
このプロセスは、LLMの基本トレーニングがベクトルデータベースから取得されたデータで補強されて応答を生成するため、検索補強生成(RAG)として知られています。
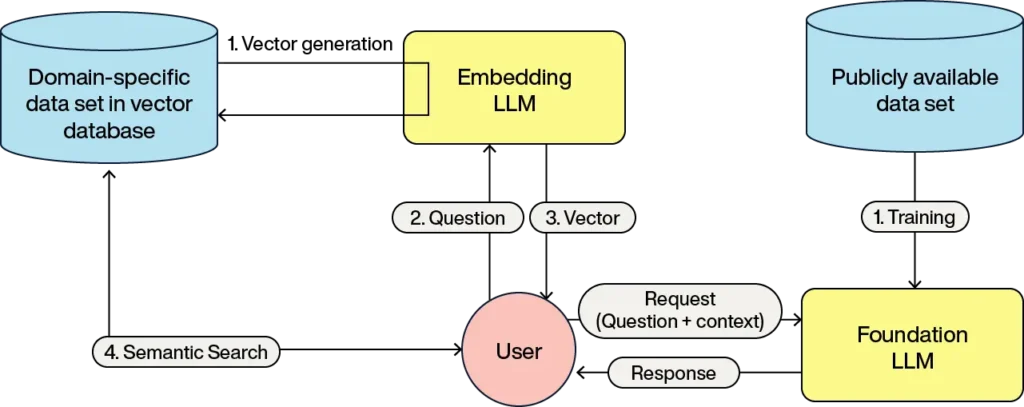
RAGのパイプラインは以下のようになります:
これらのステップはもう馴染みのあるものでしょう。
- ドメインオブジェクトのベクトルが埋め込みLLMを使用して生成され、これらのベクトルが保存されてドメインオブジェクトに関連付けられます
- ユーザーがクエリを作成し、それが埋め込みLLMに送信されます
- LLMはクエリを表すベクトルを返します
- ベクトルデータベースは最も近いベクトルに関連付けられたドメインオブジェクトを返します
- ユーザークエリは、コンテキストとしてのドメインオブジェクトと、LLMが何をすべきかの指示(プロンプトと呼ばれる)とともにLLMに渡されます
- LLMはこの情報を処理し、ユーザーへの応答を形成します
RAGはLLMの制限を解決する唯一の解決策ではないことに注意してください。
別のアプローチとして、より多くのドメイン固有の情報を提供するLLMのファインチューニングがあります。
LLMのファインチューニングは、既存の「基礎」LLMを取り、期待される結果とともに追加の注釈付きデータを与え、LLMに学習させます。
ファインチューニングは、新しい詳細が頻繁に変更されない場合に特に有用です。
例えば、ドメインの言語がトレーニングされた言語と異なる場合、英語でトレーニングされた基礎LLMは、法的言語でファインチューニングされれば、法的ドメインでより有用になるでしょう。
対照的に、RAGは、変動の激しい市場における現在の条件に基づく株式市場取引のレコメンデーションや、レコメンデーションシステムにおける商品カタログからの商品推奨など、データが急速に変化する場合により有用です。
RAGの1つの欠点は、LLMに提供されるコンテキストがLLMによって理解される必要があり、それにより数十億の追加計算と追加の時間が必要になることです。
LLMのファインチューニングとRAGは相互に排他的ではなく、多くの状況で両方を使用することが有益です。
例えば、法的ドメインでは、ファインチューニングによってLLMが法律用語を理解し出力することができ、RAGによって最新の裁判所判決を取り込み、特定のケースへの適合性を分析することができます。
Aerospikeでベクトル検索ソリューションを探る
ベクトルとベクトルデータベースは多くのAIシステムのバックボーンであり、LLMのハルシネーションを防ぎ、最新のデータに基づく応答を可能にする関連するコンテキスト情報を提供します。
構造化データまたは非構造化データをベクトル埋め込みモデルを通じて高次元ベクトルに変換することで、ベクトルデータベースは幅広い異なるソース材料に対する容易な検索機能を提供します。
小規模なベクトルデータベースの実装は非常に簡単です。
しかし、スケールのような実世界のベクトル検索には、高度なインデックス作成技術を使用するAerospikeのようなスケーラブルなソリューションを使用する必要があります。
本ブログは2025年1月21日「Making sense of vectors: Why they’re the key to smarter AI searches」の翻訳です。